S. Siegesmund, D. Nikolayeb, S. Mosch, A. Hoffmann
Profitable dimensional stone production mainly depends on the effective number of extracted blocks with a predefined size. The regularity and volume of the blocks are of critical importance. Optimization of the defined block size is therefore the most economically important task in quarrying of natural building stone. This problem is mainly connected to the quantification of joints and fractures, i.e. their spacing and orientation, since these tectonic elements affect the fragmentation of a deposit generating several blocks, not necessarily cubic in form. The problem of detecting unfractured blocks within arbitrary oriented and distributed planes (e.g. joints) cannot be solved analytically, but only effective through numerical analysis. In this article we present a brief description of a new computer program based on a numerical algorithm. The program determines the distribution, the individual shapes and volumes of in-situ blocks. The quantification of the blocks is illustrated by a number of model examples and detailed studies of quarries, which help to demonstrate that the application of the computer program could be a powerful tool for the future in exploiting dimensional stone.
1.- Introduction
Recently the demand for natural stones of different types (granite, limestone, sandstone etc.) is growing very fast. Effective manufacture of blocks with predefined dimensions requires the application of state of art extraction techniques. Furthermore, the ecological consideration also plays a major role during the mining process. Consequently, the main factors which increase profitability of a quarry of dimensional stones are block size optimization and the focus on high quality raw materials as well as the avoidance of unnecessary waste and overburden. The knowledge about the geological situation of a deposit, concerning the joint or fracture system, respectively, is essential in assuring the economic extraction of blocks from the quarry. Detailed studies of the tectonic inventory of a quarry (i.e. joints, fractures, faults) should be included in the exploration, as well as quarrying process to assure the optimal use of the material. In this context the volumes as well as the geometry and the distribution of expected raw blocks is essential. The computer program developed in this study allows the three dimensional modelling of the fragmentation of a deposit, based on the investigation of the tectonic elements, dip angles and dip directions. The problem of mutually orthogonal fracture patterns was considered by Weber et al. (2001, 2002). More recent papers (Koch-Moeck et al., 2007; Prissang et al., 2007) are also devoted to this problem. Determining the volumes of fault and fracture free parts of the stone block can not be solved in a general analytical fashion, but it can only be solved efficiently by numerical analysis.
2.- Geologic and economic considerations
The existence of individual blocks, which build up the total volume of a deposit of dimension stone, is based on the intersection of different joint or fracture systems, at all scales. Both the orientation and the respective distances have a significant influence on the prospective shapes and volumes of primary blocks. The genesis of joint and fracture systems can be multifaceted and be traced back to orogenic and epirogenic processes as well as shrinkage caused by cooling or desiccation. The existence of fractures and joints is strongly associated with thermal and strain conditions, the depth and finally the mechanical properties of the rock. Fractures are formed by exceeding the elastic limit of rocks, by compressive and tensile stresses (Palmström, 1995). Furthermore, in the case of sedimentary rocks as well as marbles, joints can be developed from bedding planes based on a change of material. Discontinuities of epirogenetic origin arise from expansion processes, which are connected with regional uplift of rock formations and therefore associated with strain release. At a local scale comparable effects can be observed by the extraction process in a deposit, due to the removal of overburden. The different kinds of discontinuities can be classified into the following groups, based on their volumetric size and their genesis: faults, joints, partings, cracks, fissures, bedding planes, shear fractures (Palmström 1995). The data collection is based on different methods, which are adapted to the individual quarry situation. For further details of discontinuity analyses see e.g. Hoffmann & Siegesmund (2007), Smith (1999) or Priest (1993). The respective volumes as well as the shapes of in-situ blocks are controlled by the three dimensional pattern of the occurring discontinuities. In general wider distances result in large-sized blocks, if the orientation of discontinuities does not diverge decisively from orthogonality. If only one or more parameters, distances or dip angles, are varying intensely, the field of application of the extracted material can be limited to low-value goods like gravel or paving stones (see Smith 1999). In the case of sedimentary rocks the possible dimensions of extracted blocks are mainly defined by the thickness of primary layering. In contrast to it, the controlling element in the case of granitic dimensional stone quarries is the spatial distribution of the joints. When the geologic or tectonic situation results in acute and led blocks, a more costs and time-consuming process occurs, since these blocks must be resized to processible stages and dimensions in order to fulfil the requirements of the modern cutting techniques. Singewald (1992) points out that the percentage of the material lost from formatting and cutting blocks decreases with increasing volume of the material. Optimal conditions occur when block volumes are between 6 and 8 m³ (Primavori, 1999). The maximum dimension of the blocks is defined by the weight of each block in terms of transport and handling during processing. Furthermore, the shape of the blocks has a significant effect on the finishing processes regarding the size of the slabs. Texture-controlled décor also has to be recognized during the extraction of blocks to ensure the quality of the desired effect of the décor.
To summarise, the economic efficiency of a deposit is controlled to a great extent by the orientation of the joint and fracture system and their spatial distribution. Therefore exact data acquisition is essential, both for exploration of new deposits as well as ongoing servicing of active quarries.
3.- Method
The newly developed computer program (see also Siegesmund et al. 2007) is able to evaluate data on the spatial distribution of e.g. joints and to give information concerning the distribution of in-situ blocks, as well as their volumes and shapes. The computer program regards the treated area of a quarry as being a parallelepiped, i.e. a geometric body composed of three pairs of parallelograms, each pair in two parallel layers. For further calculation it is necessary to divide the parallelepiped into cells or voxels, i.e. the three dimensional analogue of pixels. The voxels do not have to be cubic, but it is sufficient that all voxels are equal and similar in shape to the parallelepiped itself. The body is cross cut by joints, fractures and faults (defined as controlling elements). These elements are mathematically defined planes, which can be constructed easily based on one point and two angles. To tessellate a parallelepiped, which is intersected by a number of planes, it is necessary to define those voxels that belong to one and the same region not intersected by planes. Consequently, the different regions, resulting from the fragmentation by the controlling elements have to be identified and in the final stage be assigned different colours. The first step is to ascertain the position of each plane. This is done for each section of the parallelepiped. The identification of connected groups of voxels starts as an iterative process. Starting with the first voxel the program checks whether the neighbours belong to the same region or not. After all the voxels belonging to the same region as the first one are coloured, a new uncoloured voxel is chosen and assigned a new colour. This procedure is repeated until the whole parallelepiped is coloured. The bottom line is a clearly arranged coloured description of the three dimensional segmentation of the modelled block. After the tessellation is modelled, the volumes of each region can be easily calculated. Besides the mathematical modelling the computer program allows for multiple rotations in all directions in space with a free choice of intersections parallel to the surfaces, simultaneously. Thus the user is able to examine the quarry situation from all possible perspectives. The total volume of voxels that are assigned belong to planes or joints that do not vanish because of the finite voxel volume. However, the relative volume decreases with an increase in the number of voxels. On the other hand, natural joints also have some finite size. So it could be argued that for practical purposes this is a more adequate description than in the case of a mathematical object such as planes which have zero volume. Digital photos have a finite number of pixels and colours and nevertheless no one doubts, that they correctly reflect reality. Computing time is very closely connected to the voxel size or number of voxels under consideration. So for primary tessellation and volume estimation in the field, a small number of voxels is preferred.
4.- Computer and natural models
The model examples presented below illustrate different aspects of the suggested approach. In the following three models examples are presented which differ in its complexity with regards to the segmentation due to cross-cutting planes:
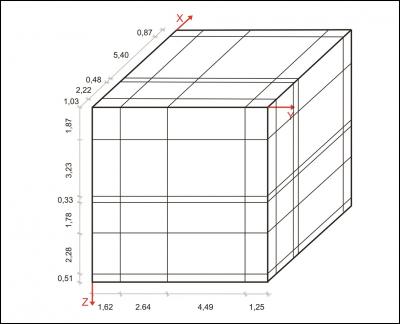
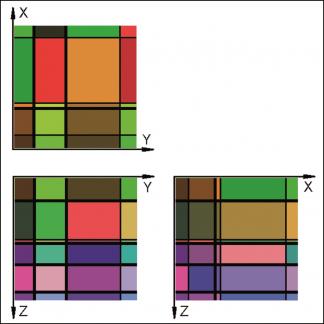
- (i) a completely orthogonal distribution of segmenting elements (Fig. 1-3)

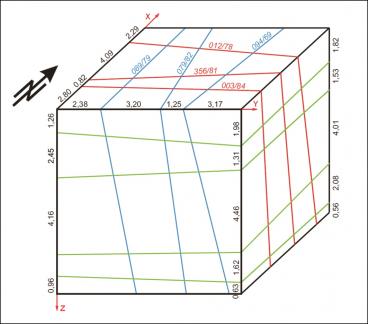
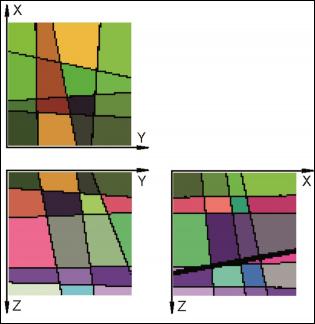
- (ii) an example in which joints are slightly different from the orthogonal case (Fig. 4-6)
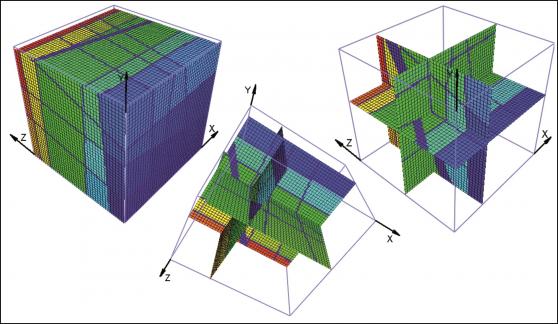
- (iii) a model body of complex structure with an arbitrary distribution of segmenting elements (Fig. 7-9)
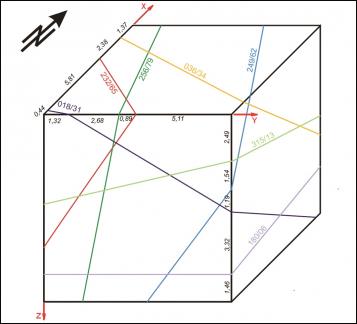
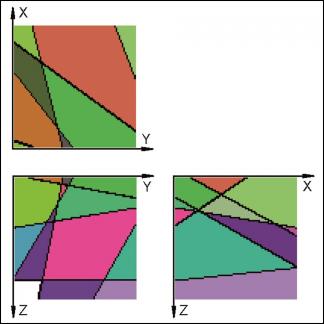
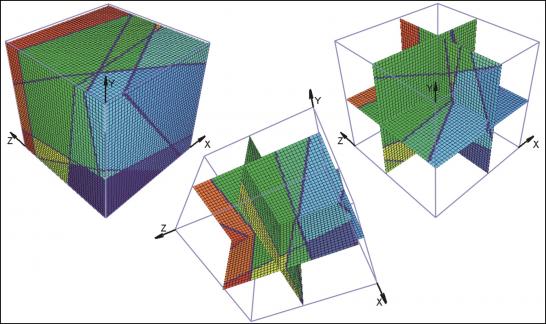
For each case the starting point is a sketch of the artificial block with its cross-cutting elements (Fig. 1, 4, 7). As one can see, the included data concerning the distances on the three axes and the orientation of planes can be easily investigated in the field. For the completely orthogonal case the volumes of each in-situ block can be easily computed without numerical error. This example was only used to verify accuracy of the method. For modelling purposes each block is divided into 128x128x128 voxels which correspond to an edge length of 7.8 cm for each individual voxel. Volume error with this particular voxel size is less than one percent. On figures 2, 5, 8 traces of all joints are marked with black lines. Figures 3, 6 and 9 give examples of the multivariate rotation of the modelled block in all directions of space. Furthermore, the possibility of free choice of intersection is demonstrated. At the computer the modelled block as well as the intersections can be moved interactively. The efficiency and accuracy of the computer program is being currently tested in different dimensional stone quarries. One of the investigated quarries is located near by Arzachena, N Sardinia (Italy), where the granitic commercial grade Rigo di San Antonio is obtained. The rock is medium- to coarse- grained and exhibits locally weak texture. In general it shows a typical joint pattern for granitic bodies. Besides several straight linear planes, the block is segmented by some non linear fractures resulting from exfoliation processes as well as smaller discontinuities often associated with irregular structures. These non-linear elements demonstrate highly complex patterns, which cannot be reproduced easily in a mathematical sense. Hence, for present purposes to illustrate the method of operation of the computer program the data selection has been carried out on the more or less main linear elements. Due to an overburden cover on the top of the considered block the data acquisition has been conducted in the present case on two vertical quarry faces normal to each other (Fig. 10). The collection of data has been carried out along free-standing vertical as well as horizontal profiles. If possible the measurements of distances between the separation planes are accompanied by recordings of the spatial orientation of them (Fig. 10).

For the modelling process a voxel edge length of 12.5 cm was chosen. The primary output of computation is given in figure 11. Although the present example demonstrates a simplified model of the real situation, the three successive vertical intersections (front surface, mid-intersection and rear surface) already indicate the complexity of the joint pattern (Fig. 11, right).
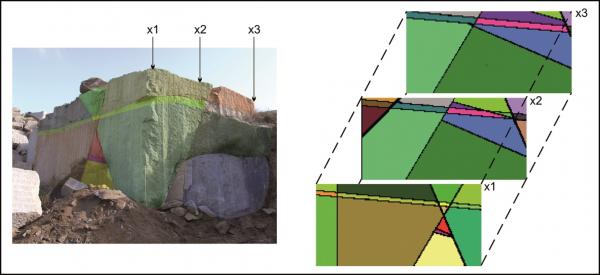
The chosen intersections point to the occurrence of bigger in-situ blocks within the rear parts of the quarry (dark green colour). Applying the possibility of free rotation with the computer program, the possible presence of these bodies can be shown. However, the modelling remains one possible interpretation of the real situation. This is due to the lack of information about the interaction between the multiple cross-cutting of discontinuities inside the considered block.
5.- Conclusions
Based on the multiple possibilities the computer program 3D-BlockExpert is an effective tool for an increasing, target-oriented extraction of dimensional stones with respect to both economic as well as ecological aspects. Therefore, the field of application ranges from the stage of exploration to the improvement of the actual mining processes. Recently the quarrying of dimensional stones is often carried out without a detailed knowledge of the geological background and quality of the deposits. This fact results in inadequate mining strategies connected with useless wastages of material, since in many cases a much higher recovery of raw blocks could be reached in consideration of all geologically influencing factors, especially the fracture system. The program 3D-BlockExpert processes data of the discontinuity system such as fracture spacing and fracture orientation and provides a multivariate modelling for the optimization of the early exploration phase. Due to the detection of large volume blocks the application of the program can identify areas recoverable for the dimensional stone industry defined by the possible extraction of well-dimensioned raw blocks. Other parts of deposits, in particular multiple cross-cut sections with a high amount of irregular small-scaled in-situ blocks, can be excluded in advance or identified for the mining of alternative products such as gravel and grit, respectively. Consequently, the concise visualization can finally support the process of licensures due to a significant verification of the deposit reserves and its related economic value. A significant factor during the actual mining process is the maximal utilization of the recoverable areas to optimize the raw block extraction rate. Disregard of the distribution of separation planes might result in the useless destruction of a highly valuable material. The detailed information about the course of these elements given by the computer program could facilitate any decision regarding the further mining activities. If procurable, the extraction of blocks should be adapted to the geo-structural situation to avoid increased irregular, acute-angled blocks. As already mentioned, the formatting of correspondingly shaped bodies to raw blocks is connected with additional time- and cost-consuming procedures. Eliminating these problems, the extraction rate of well dimensioned raw blocks can be enhanced, leading to an increase of the economic out-put of a quarry. To summarize, the assessment of a joint and fracture system in a deposit for dimensional stones via the here presented program 3D-BlockExpert provides a forward-looking approach for sustainable quarry management. In the future the demand of dimensional stone as a multifunctional element for construction purposes will increase continuously, which implies that environmental considerations during the exploration and mining process must be guaranteed. It will be essential to make the best possible use of the high quality material and to minimize the impact of quarrying activities to nature. The realization of these objectives can be supported extensively by means of computer based scientific investigations.
Acknowledgements: this work is supported by DFG grant No GZ: 436 RUS 17/23/06
References:
- Hoffmann, A., Siegesmund, S. (2007): Investigation of dimension stones in Thailand: an approach to a methodology for the assessment of stone deposits. In: S. Siegesmund & A. Ehling (Eds.): Rohstoff Naturstein. Zeitschrift der deutschen Gesellschaft für Geowissenschaften.
- Koch-Moeck, M., Germann, K. (2007): Geowissenschaftliche Optimierung der untertägigen Gewinnung von Marmor. - In: S. Siegesmund & A. Ehling (Eds.): Rohstoff Naturstein. Zeitschrift der deutschen Gesellschaft für Geowissenschaften.
- Palmström, A. (1995): RMi - a rock mass characterisation system for rock engineering purposes. - Ph.D. thesis of the University of Oslo, Norway.
- Priest, S.D. (1993): Discontinuity analysis for rock engineering. –Chapman and Hall, London, 473 p.
- Primavori, P. (1999): Planet stone. Giorgio 7th Edition S.A.S., Verona, 326 p.
- Prissang, R., Hella, P., Lehtimäki, T., Saksa, P., Nummela, J., Vuento A. (2007): Lokalisierung ungestörter Blöcke in größeren Gesteinsmassen. - In: S. Siegesmund & A. Ehling (Eds.): Rohstoff Naturstein. Zeitschrift der deutschen Gesellschaft für Geowissenschaften.
- Siegesmund, S., Nikolayev, D., Hoffmann, A., S. Mosch (2007): 3D-Block-Expert. Naturstein, 5
- Singewald, C. (1992): Naturstein - Exploration und Gewinnung. - Rudolf Mueller, Bad Bentheim
- Smith, M.R. (Ed.) (1999): Stone: Building stone, rock fill and armour stone in construction.- Geological Society of London, Engineering Geology, Special Publications, Volume 16.
- Weber, J., Dehnhart, J., Lepper, J. (2001): Trennflachenanalyse zur Vorratsermittlung von Naturwerkstein Lagerstätten. Zeitschrift für Angewandte Geologie 47(2), 74-78.
- Weber, J., Lepper, J. (2002): Depositional environment and diagenesis as controlling factors for petro-physical properties and weathering resistance of siliciclastic dimension stones: integrative case study on the ‘Wesersandstein’ (northern Germany, Middle Bundsandstein). - In: Siegesmund, S., Weiss, T., Vollbrecht, A. (Eds.): Natural stone, Weathering phenomena, Conservation strategies and Case studies. Geological Society of London, Special Publications 205, 103-114.
- Zeitschrift der deutsche Gesellschaft für Geowissenschaften 2007, 158, vol. 3
