S. Siegesmund, D. Nikolayeb, S. Mosch, A. Hoffmann
Una producción rentable de piedra natural depende principalmente del número efectivo de bloques extraídos de un tamaño predefinido. La regularidad y el volumen de los bloques tienen una importancia crítica. La optimización del tamaño del bloque definido es por tanto la tarea económica más importante en lo que a extracción de bloques de piedra para construcción se refiere. Este problema está principalmente conectado a la cuantificación de las juntas y fracturas, esto es, su espaciado y orientación, ya que estos elementos tectónicos afectan a la fragmentación de un depósito generando varios bloques, no necesariamente de forma cúbica. El problema de la detección bloques sin fracturas dentro de unos planos distribuidos y orientados de forma arbitraria sólo se puede resolver mediante un análisis numérico. En este artículo presentamos una breve descripción de un nuevo programa informático basado en algoritmos numéricos. El programa determina la distribución, las formas y los volúmenes de los bloques in situ. La cuantificación de los bloques está ilustrada con varios modelos de ejemplos y detallados estudios de las canteras, que ayudan a demostrar que la aplicación de este programa informático puede ser una poderosa herramienta para el futuro en la explotación de la piedra ornamental.
1.- Introducción
Recientemente, la demanda de piedra natural de diferentes tipos (granito, caliza, arenisca, etc.) está creciendo muy deprisa. La elaboración efectiva de bloques con dimensiones predefinidas requiere la aplicación de técnicas de extracción de tecnología punta. Además, las consideraciones ecológicas también juegan un papel importante durante el proceso de extracción. Por lo tanto, los factores que hacen aumentar la rentabilidad de una cantera de piedras dimensionales son la optimación del tamaño de los bloques y el enfoque en la alta calidad de los materiales, así como evitar la creación de desechos innecesarios. El conocimiento de la situación geológica de un depósito en lo que se refiere a juntas o fracturas es esencial para asegurar la extracción económica de los bloques de la cantera. En la exploración deberían incluirse estudios detallados del inventario tectónico de una cantera (juntas, fracturas, fallos), así como el proceso de extracción para asegurar el aprovechamiento óptimo del material. En este contexto resultan esenciales los volúmenes, la geometría y la distribución de los bloques previstos. El programa informático desarrollado en este estudio permite el modelado en tres dimensiones de la fragmentación de un depósito, basado en la investigación de elementos tectónicos, ángulos y direcciones. El problema del modelo de fractura ortogonal fue tratado por Weber et al. (2001-2002). Informes más recientes (Koch-Moeck et al. 2007, Prissang et al., 2007) también lo han tratado. Determinar los volúmenes de fallos y fracturas de manera eficiente es algo que sólo se puede hacer mediante análisis numéricos.
2.- Consideraciones geológicas y económicas
La existencia de bloques individuales que constituyen el volumen total de un depósito de piedra dimensional, se basa en la intersección de diferentes sistemas de uniones o fracturas en todas las escalas. Tanto la orientación como las distancias respectivas tienen una significativa influencia en la forma y volumen de bloques primarios. Las génesis de los sistemas de uniones y fracturas pueden ser multifacéticas y estar trazadas desde los procesos orogénicos y epirogénicos, así como la reducción ocasionada por enfriamiento o desecación. La existencia de fracturas y juntas está fuertemente asociada a las condiciones termales y de presión, a la profundidad y a las propiedades mecánicas de la roca. Las fracturas se forman por el exceso del límite de elasticidad de las rocas (Palmström, 1995). Además, en el caso de rocas sedimentarias y mármoles, las uniones se pueden originar desde el nivel de las bancadas en base a un cambio de material. Las discontinuidades de origen epirogénico surgen de los procesos de expansión, que están conectados con la sustentación regional de las formaciones rocosas y por lo tanto asociados a la salida de presión. A escala local se pueden observar efectos comparables en el proceso de extracción en un depósito, debido a la eliminación de sobrecarga. Los diferentes tipos de discontinuidades se pueden clasificar en los siguientes grupos, basados en sus tamaños volumétricos y sus génesis: fallos, uniones, separaciones, roturas, fisuras y planos de bancadas (Palmström, 1995). La recopilación de datos se basa en diferentes métodos, adaptados a la situación individual de cada cantera. Para más detalles sobre análisis de discontinuidad ver Hoffmann & Siegesmund (2007), Smith (1999) o Priest (1993). Los respectivos volúmenes y las formas de los bloques in situ están controlados por tres patrones dimensionales de las discontinuidades. En general, distancias más amplias se traducen en bloques de mayor tamaño, si la orientación de las discontinuidades no diverge de manera decisiva de la ortogonalidad. Si sólo uno o más parámetros, distancias o ángulos varían intensamente, el campo de aplicación del material extraído puede ser limitado a elementos de bajo valor, como gravilla o adoquines (ver Smith 1999). En el caso de rocas sedimentarias, las posibles dimensiones de los bloques están definidas principalmente por el grosor de la capa primaria. En contraste a esto, el elemento a controlar en el caso de canteras de materiales graníticos es la distribución espacial de las juntas. Cuando las condiciones geológicas o tectónicas se traducen en bloques grandes o salientes, como esos bloques deben ser redimensionados para proceder a la su procesado de acuerdo a los requerimientos de las modernas tecnologías de corte, aumenta el coste y el tiempo necesarios para su elaboración. Singewald (1992) destaca que el porcentaje de material que se pierde con la formación y corte de los bloques disminuye con el aumento del volumen del material Las condiciones óptimas se dan cuando el volumen de los bloques está entre 6 y 8 m3 (Primavori, 1999). La dimensión máxima de los bloques viene definida por el peso de cada bloque en términos de transporte y manipulado durante el procesado. Además, la forma de los bloques tiene un efecto significativo sobre el proceso de acabado en cuanto al tamaño de las tablas. El control de la textura también tiene que realizarse durante la extracción de los bloques para asegurar la calidad del efecto deseado. Para resumir, la eficiencia económica de un depósito está controlada sobre todo por la orientación del sistema de juntas y fracturas y su distribución espacial. Por lo tanto es esencial tener datos exactos, tanto para la exploración de nuevos depósitos como para el control del funcionamiento de las canteras activas.
3.- Método
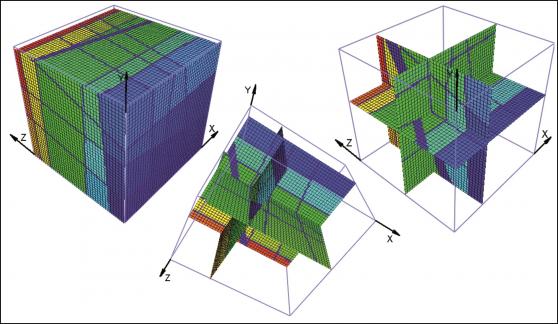
El recientemente desarrollado programa informático (ver Siegesmund et al. 2007) es capaz de evaluar los datos de la distribución espacial de las juntas y dar información acerca de la distribución de los bloques in-situ y de sus volúmenes y formas. El programa considera la zona a examinar de la cantera como un paralelepípedo, es decir un cuerpo geométrico compuesto de tres pares de paralelogramas, cada par en dos capas paralelas. Para un cálculo posterior, es necesario dividir el paralelepípedo en celdas o voxels, es decir, el equivalente tridimensional de los píxeles. Los voxels no tienen que ser cúbicos, es suficiente que todos sean iguales y similares en forma al propio paralelepípedo. El cuerpo está atravesado por juntas, fracturas y fallos (definidos como elementos de control). Estos elementos son planos matemáticamente definidos, que se pueden construir fácilmente con un punto y dos ángulos. Para teselar un paralelepípedo, que está intersectado por un número de planos, es necesario definir aquellos voxels que pertenecen a una y la misma zona no intersectada por planos. En consecuencia, hay que identificar las diferentes zonas resultantes de la fragmentación hecha por los elementos de control y asignar a cada una un color diferente en la fase final. El primer paso es averiguar la posición de cada plano. Esto se hace en cada sección del paralelepípedo. La identificación de grupos conectados de voxels comienza como un proceso iterativo. Comenzando por el primer voxel, el programa comprueba si los voxels contiguos pertenecen o no a la misma zona. Todos los voxels pertenecientes a la misma zona se colorean, luego se elige otro voxel y se le asigna un nuevo color. Este procedimiento se repite hasta que queda coloreado todo el paralelepípedo. La línea inferior es una descripción de las tres segmentaciones dimensionales del bloque modelo. Una vez hecho esto, se puede calcular fácilmente el volumen de cada región. Además del modelo matemático, el programa permite múltiples rotaciones en todas las direcciones espaciales con una elección libre y simultánea de intersecciones paralelas a las superficies. Por lo tanto, el usuario puede examinar la situación de la cantera desde todas las perspectivas posibles. El volumen total de los voxels que se han asignado pertenece a planos o juntas que no desaparecen debido al volumen finito del voxel. Sin embargo, el volumen relativo decrece con un aumento del número de voxels. Por otro lado, las juntas naturales también tienen un tamaño finito. Por lo tanto, se puede argumentar que a efectos prácticos ésta es una descripción más adecuada que en el caso de un objeto matemático como por ejemplo un plano, que tiene cero volumen. Las fotos digitales tienen un número finito de píxeles y colores pero nadie duda de que reflejan correctamente la realidad. El tiempo para calcular está muy estrechamente conectado al tamaño del voxel o al número de voxels en consideración. Por eso es preferible utilizar un número pequeño de voxels para la primera estimación del volumen.
4.- Modelos informáticos y naturales
Los modelos presentados a continuación ilustran distintos aspectos de lo expuesto hasta ahora. Los siguientes tres ejemplos difieren en su complejidad en cuanto a la segmentación por sus planos de corte:
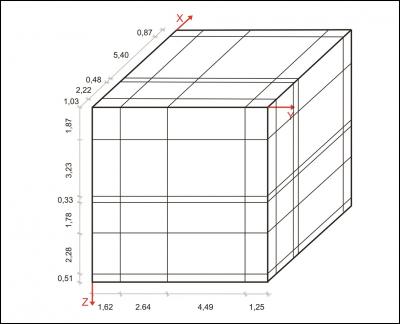
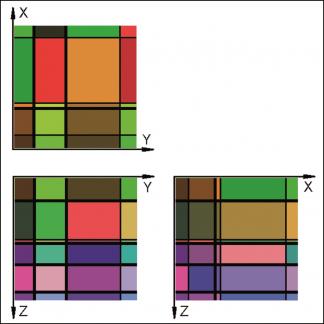
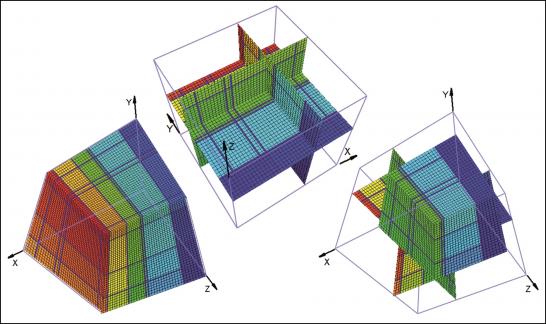
- (I) una distribución completamente ortogonal de los elementos de segmentación (Fig. 1-3)
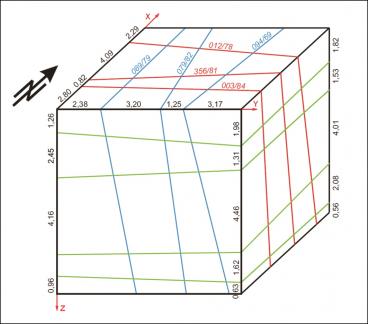
- (II) un ejemplo en el que las juntas son ligeramente diferentes del caso ortogonal (Fig. 4-6)
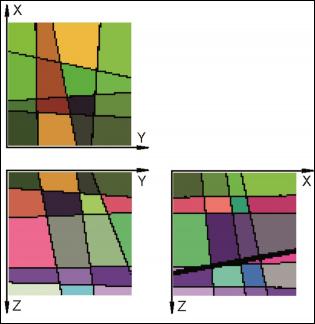
- (III) un cuerpo de estructura compleja con una distribución arbitraria de los elementos de segmentación (Fig. 7-9)
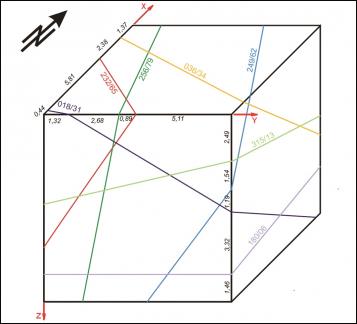
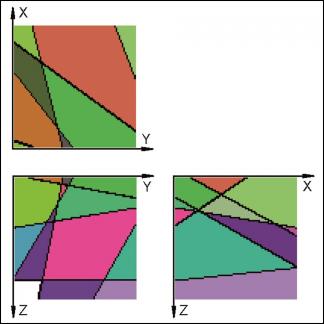
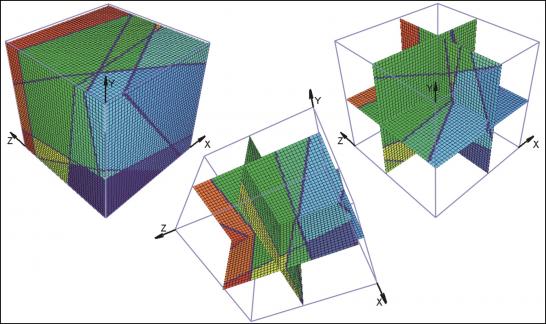
Para cada caso, el punto de comienzo es un boceto del bloque artificial con sus elementos de intersección (Fig., 1, 4, 7). Como podemos ver, los datos incluidos relativos a las distancias en los tres ejes y la orientación de los planos pueden ser fácilmente investigados en el campo. En el caso del modelo completamente ortogonal, los volúmenes de cada bloque in-situ se pueden computar fácilmente sin errores numéricos. Este ejemplo sólo se usó para verificar la precisión del método. A efectos de modelo, cada bloque se divide en 128x128x128 voxels, que corresponden a una longitud de perfil de 7,8 cm. para cada voxel individual. El error de volumen de este particular tamaño de voxel es menos del 1%. En las figuras 2, 5, 8, los trazos de todas las juntas están marcados con líneas negras. Las figuras 3, 6 y 9 ofrecen ejemplos de rotación multivariada de los bloques modelados en todas las direcciones del espacio. Además, se demuestra la posibilidad de libre elección de intersecciones. En el ordenador, el bloque modelado y las intersecciones se pueden mover de modo interactivo. La eficiencia y precisión del programa informático se está probando en la actualidad en diferentes canteras de piedra. Una de ellas está ubicada cerca de Arzachena, N. Sardinia (Italia), de donde se extrae el granito Rigo de San Antonio. Esta roca es de grano medio a grueso y muestra textura localmente débil. En general muestra un patrón de unión típico de cuerpos graníticos. Además de varios planos lineales rectos, el bloque está segmentado por algunas fracturas no lineales resultado del proceso de exfoliación y de pequeñas discontinuidades a menudo asociadas a estructuras irregulares. Esos elementos no lineales muestran patrones altamente complejos, que no se pueden reproducir fácilmente en sentido matemático. De ahí que, con el fin de ilustrar el método de operación del programa, la selección de datos se llevó a cabo sobre los principales elementos más o menos lineales. Debido a una tapa de sobrecarga en lo alto del bloque tratado, la obtención de datos, en este caso, se ha hecho sobre dos caras verticales de la cantera (Fig. 10).

La recopilación de datos se hizo a lo largo de perfiles verticales y horizontales independientes. Cuando es posible, las medidas de las distancias entre los planos de separación van acompañadas de datos de su orientación espacial (Fig. 10). Para el modelo se eligió una longitud de perfil de voxel de 12,5 cm. El rendimiento primario de computación se ve en la figura 11. Aunque este ejemplo representa un modelo simplificado de la situación real, las tres intersecciones verticales sucesivas (superficie frontal, intersección media y superficie posterior) ya indican la complejidad del patrón de unión (Fig. 11, derecha).
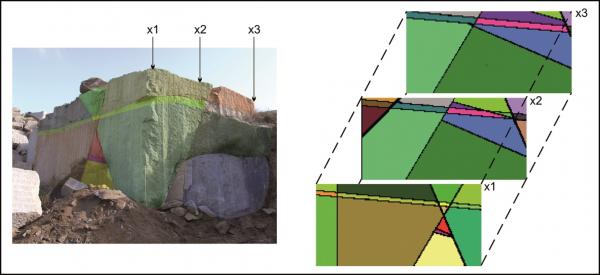
El punto de intersección escogido señala la existencia de bloques in situ mayores en la zona posterior de la cantera (color verde oscuro). Aplicando la posibilidad de libre rotación con el programa, se muestra la posible presencia de esos cuerpos. Sin embargo, el modelo sigue siendo una posible interpretación de la situación real. Esto se debe a la falta de información sobre la interacción entre las múltiples líneas de corte de discontinuidades dentro del bloque.
5.- Conclusiones
Teniendo en cuenta sus múltiples posibilidades, el programa informático 3D-BlockExpert constituye una herramienta efectiva en la extracción de piedra dimensional desde el punto de vista económico y ecológico. El campo de aplicación va desde la exploración hasta la mejora del proceso de extracción. La extracción de piedra dimensional a menudo se hace sin tener un conocimiento detallado de las características geológicas y de la calidad de los yacimientos. Esto se traduce en estrategias inadecuadas de extracción, que implican pérdida de material, porque en muchos casos el aprovechamiento podría haber sido mucho mayor si se hubieran tenido en cuenta factores geológicos influyentes, sobre todo los sistemas de fracturas. El programa 3D-BlockExpert procesa datos del sistema de discontinuidad tales como distancia entre fracturas y orientación de las mismas y suministra varios modelos para la optimización desde la fase de exploración. Debido a la detección de bloques de gran volumen, la aplicación del programa puede identificar áreas recuperables para la industria de la piedra dimensional definidas por la posible extracción de bloques bien dimensionados. Otras partes de los yacimientos, en concreto secciones multisegmentadas con una elevada cantidad de bloques pequeños in-situ, pueden ser excluidas por adelantado o identificadas para la producción de productos alternativos, tales como gravilla y arenilla, respectivamente. Por lo tanto, la visualización concisa puede finalmente apoyar el proceso de licencias debido a la verificación de las reservas que tiene el depósito y a su consiguiente valor económico. Un factor importante dentro de la minería es la máxima utilización de las zonas recuperables para optimizar la tasa de extracción. No tener en cuenta la distribución de los planos de separación puede traer como consecuencia la destrucción de un material valioso. La información detallada sobre todos esos elementos que proporciona el programa facilitaría cualquier decisión acerca de las futuras actividades mineras. Siempre que sea posible, la extracción de los bloques debe adaptarse a la situación geo-estructural para evitar los bloques irregulares. Como ya se ha mencionado, la transformación de los bloques irregulares en bloques regulares va unida a un aumento de coste y de tiempo de elaboración. Eliminando esos problemas se puede aumentar la tasa de extracción de bloques bien dimensionados, con lo que se lograría un aumento de la producción económica de una cantera. Para resumir, la evaluación de un sistema de juntas y fracturas en un yacimiento de piedra a través del programa 3D-BlockExpert aquí presentado proporciona la posibilidad de hacer una planificación de cara a un máximo rendimiento de la cantera. En el futuro, la demanda de piedra dimensional como un elemento multifuncional para la construcción incrementará continuamente, lo que implica que hay que garantizar que se cumplen los requisitos medioambientales durante los procesos de exploración y de extracción. Será esencial hacer el mejor uso posible del material de alta calidad y minimizar el impacto de las tareas de extracción en la naturaleza. Las investigaciones científicas basadas en la informática pueden ser un gran apoyo a la realización de estos objetivos.
Agradecimientos: este trabajo ha contado con el apoyo de DFG grant No GZ: 436 RUS 17/23/06
Referencias:
- Hoffmann, A., Siegesmund, S. (2007): Investigation of dimension stones in Thailand: an approach to a methodology for the assessment of stone deposits. In: S. Siegesmund & A. Ehling (Eds.): Rohstoff Naturstein. Zeitschrift der deutschen Gesellschaft für Geowissenschaften.
- Koch-Moeck, M., Germann, K. (2007): Geowissenschaftliche Optimierung der untertägigen Gewinnung von Marmor. - In: S. Siegesmund & A. Ehling (Eds.): Rohstoff Naturstein. Zeitschrift der deutschen Gesellschaft für Geowissenschaften.
- Palmström, A. (1995): RMi - a rock mass characterisation system for rock engineering purposes. - Ph.D. thesis of the University of Oslo, Norway.
- Priest, S.D. (1993): Discontinuity analysis for rock engineering. –Chapman and Hall, London, 473 p.
- Primavori, P. (1999): Planet stone. - Giorgio 7th Edition S.A.S., Verona, 326 p.
- Prissang, R., Hella, P., Lehtimäki, T., Saksa, P., Nummela, J., Vuento A. (2007): Lokalisierung ungestörter Blöcke in größeren Gesteinsmassen. - In: S. Siegesmund & A. Ehling (Eds.): Rohstoff Naturstein. Zeitschrift der deutschen Gesellschaft für Geowissenschaften.
- Siegesmund, S., Nikolayev, D., Hoffmann, A., S. Mosch (2007): 3D-Block-Expert. Naturstein, 5
- Singewald, C. (1992): Naturstein - Exploration und Gewinnung. - Rudolf Mueller, Bad Bentheim
- Smith, M.R. (Ed.) (1999): Stone: Building stone, rock fill and armour stone in construction.- Geological Society of London, Engineering Geology, Special Publications, Volume 16.
- Weber, J., Dehnhart, J., Lepper, J. (2001): Trennflachenanalyse zur Vorratsermittlung von Naturwerkstein Lagerstätten. Zeitschrift für Angewandte Geologie 47(2), 74-78.
- Weber, J., Lepper, J. (2002): Depositional environment and diagenesis as controlling factors for petro-physical properties and weathering resistance of siliciclastic dimension stones: integrative case study on the ‘Wesersandstein’ (northern Germany, Middle Bundsandstein). - In: Siegesmund, S., Weiss, T., Vollbrecht, A. (Eds.): Natural stone, Weathering phenomena, Conservation strategies and Case studies. Geological Society of London, Special Publications 205, 103-114.
- Zeitschrift der deutsche Gesellschaft für Geowissenschaften 2007, 158, vol. 3
